what happens to the rate when [a] is doubled if x=0
two.8: Second-Order Reactions
- Page ID
- 1440
Many of import biological reactions, such as the formation of double-stranded Dna from two complementary strands, can be described using second gild kinetics. In a second-order reaction, the sum of the exponents in the rate police force is equal to two. The two most mutual forms of 2nd-order reactions will be discussed in detail in this section.
To describe how the rate of a second-order reaction changes with concentration of reactants or products, the differential (derivative) rate equation is used also as the integrated rate equation. The differential charge per unit police force can prove us how the rate of the reaction changes in fourth dimension, while the integrated rate equation shows how the concentration of species changes over fourth dimension. The latter class, when graphed, yields a linear function and is, therefore, more than convenient to wait at. However, both of these equations can exist derived from the to a higher place expression for the reaction rate. Plotting these equations can also help us determine whether or not a certain reaction is second-society.
Case 1: Identical Reactants
Two of the same reactant (\(\ce{A}\)) combine in a single elementary footstep.
\[\begin{align} \ce{A} + \ce{A} &\ce{->} \ce{P} \label{case1a} \\[4pt] \ce{2A} &\ce{->} \ce{P} \label{case1b} \end{align}\]
The reaction rate for this step can be written as
\[\text{Rate} = - \dfrac{one}{2} \dfrac{d[A]}{dt} = + \dfrac{d[P]}{dt} \nonumber\]
and the rate of loss of reactant \(\ce{A}\)
\[\dfrac{dA}{dt}= -1000[A][A] = -k[A]^ii \label{2ndlaw}\]
where \(k\) is a second order rate abiding with units of G-one min-i or M-ane s-one. Therefore, doubling the concentration of reactant \(\ce{A}\) will quadruple the rate of the reaction. In this particular case, another reactant (\(B\)) could be nowadays with \(A\); however, its concentration does non affect the charge per unit of the reaction, i.e., the reaction order with respect to B is zero, and we can express the rate law as \(five = m[A]^2[B]^0\).
Integration of Equation \ref{2ndlaw} yields
\[ \dfrac{ane}{[A]} = \dfrac{1}{[A]_0}+kt\]
which is hands rearranged into a form of the equation for a direct line and yields plots similar to the one shown below.

The half-life is given by
\[ t_{1/2}=\dfrac{1}{k[A_o]}\]
Discover that the half-life of a second-gild reaction depends on the initial concentration, in contrast to offset-order reactions. For this reason, the concept of one-half-life for a second-social club reaction is far less useful. Reaction rates are discussed in more than detail here. Reaction orders are defined here. Here are explanations of zero and first order reactions.
For reactions that follow Equation \ref{case1a} or \ref{case1b}, the rate at which \(\ce{A}\) decreases tin be expressed using the differential charge per unit equation.
\[-\dfrac{d[A]}{dt} = k[A]^two\]
The equation can then be rearranged:
\[\dfrac{d[A]}{[A]^2} = -k\,dt\]
Since we are interested in the change in concentration of A over a flow of time, nosotros integrate betwixt \(t = 0\) and \(t\), the time of involvement.
\[ \int_{[A]_o}^{[A]_t} \dfrac{d[A]}{[A]^2} = -k \int_0^t dt\]
To solve this, we apply the following dominion of integration (power rule):
\[\int \dfrac{dx}{x^2} = -\dfrac{ane}{x} + constant\]
We then obtain the integrated rate equation.
\[\dfrac{1}{[A]_t} - \dfrac{1}{[A]_o} = kt\]
Upon rearrangement of the integrated rate equation, nosotros obtain an equation of the line:
\[\dfrac{1}{[A]_t} = kt + \dfrac{1}{[A]_o}\]
The crucial function of this process is not understanding precisely how to derive the integrated charge per unit constabulary equation, rather it is of import to empathise how the equation directly relates to the graph which provides a linear human relationship. In this case, and for all 2d order reactions, the linear plot of \(\dfrac{one}{[A]_t}\) versus time will yield the graph below.
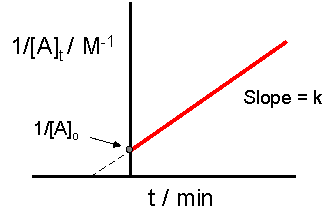
This graph is useful in a diverseness of ways. If we only know the concentrations at specific times for a reaction, we can attempt to create a graph similar to the one above. If the graph yields a straight line, then the reaction in question must be second order. In addition, with this graph nosotros can find the slope of the line and this slope is \(yard\), the reaction constant. The slope tin can be plant be finding the "rise" and and then dividing it by the "run" of the line. For an example of how to find the slope, please see the example section below. In that location are culling graphs that could be drawn.
The plot of \([A]_t\) versus fourth dimension would result in a directly line if the reaction were zeroth order. It does, however, yield less data for a 2nd order graph. This is because both the graphs of a commencement or second order reaction would await similar exponential decays. The only obvious departure, as seen in the graph below, is that the concentration of reactants approaches zip more slowly in a second-order, compared to that in a outset gild reaction.

Case 2: Second Order Reaction with Multiple Reactants
Ii different reactants (\(\ce{A}\) and \(\ce{B}\)) combine in a single uncomplicated step:
\[A + B \longrightarrow P \label{case2}\]
The reaction rate for this step can exist written every bit
\[\text{Rate} = - \dfrac{d[A]}{dt}= - \dfrac{d[B]}{dt}= + \dfrac{d[P]}{dt}\]
and the rate of loss of reactant \(\ce{A}\)
\[ \dfrac{d[A]}{dt}= - one thousand[A][B]\]
where the reaction gild with respect to each reactant is one. This means that when the concentration of reactant A is doubled, the rate of the reaction will double, and quadrupling the concentration of reactant in a separate experiment volition quadruple the rate. If nosotros double the concentration of \(\ce{A}\) and quadruple the concentration of \(\ce{B}\) at the same time, then the reaction rate is increased by a factor of viii. This human relationship holds true for any varying concentrations of \(\ce{A}\) or \(\ce{B}\).
Equally before, the rate at which \(A\) decreases can be expressed using the differential charge per unit equation:
\[ \dfrac{d[A]}{dt} = -m[A][B] \nonumber \]
Ii situations tin exist identified.
Situation 2a: \([A]_0 \neq [B]_0\)
Situation 2a is the state of affairs that the initial concentration of the two reactants are non equal. Let \(10\) be the concentration of each species reacted at time \(t\).
Let \( [A]_0 =a\) and \([B]_0 =b\), then \([A]= a-x\) ;\( [B]= b-x\). The expression of rate police becomes:
\[-\dfrac{dx}{dt} = -k([A]_o - x)([B]_o - x)\nonumber \]
which tin be rearranged to:
\[\dfrac{dx}{([A]_o - x)([B]_o - x)} = kdt\nonumber \]
Nosotros integrate between \(t = 0\) (when \(10 = 0\)) and \(t\), the fourth dimension of interest.
\[ \int_0^x \dfrac{dx}{([A]_o - 10)([B]_o - x)} = thou \int_0^t dt \nonumber \]
To solve this integral, we use the method of partial fractions.
\[ \int_0^x \dfrac{1}{(a - x)(b -x)}dx = \dfrac{1}{b - a}\left(\ln\dfrac{1}{a - x} - \ln\dfrac{ane}{b - x}\right)\nonumber \]
Evaluating the integral gives us:
\[ \int_0^x \dfrac{dx}{([A]_o - x)([B]_o - ten)} = \dfrac{1}{[B]_o - [A]_o}\left(\ln\dfrac{[A]_o}{[A]_o - x} - \ln\dfrac{[B]_o}{[B]_o - ten}\right) \nonumber \]
Applying the rule of logarithm, the equation simplifies to:
\[\int _0^10 \dfrac{dx}{([A]_o - x)([B]_o - 10)} = \dfrac{1}{[B]_o - [A]_o} \ln \dfrac{[B][A]_o}{[A][B]_o} \nonumber \]
We then obtain the integrated rate equation (under the condition that [A] and [B] are not equal).
\[ \dfrac{1}{[B]_o - [A]_o}\ln \dfrac{[B][A]_o}{[A][B]_o} = kt \nonumber \]
Upon rearrangement of the integrated charge per unit equation, we obtain:
\[ \ln\dfrac{[B][A]_o}{[A][B]_o} = k([B]_o - [A]_o)t \nonumber \]
Hence, from the last equation, nosotros can run into that a linear plot of \(\ln\dfrac{[A]_o[B]}{[A][B]_o}\) versus time is characteristic of second-order reactions.
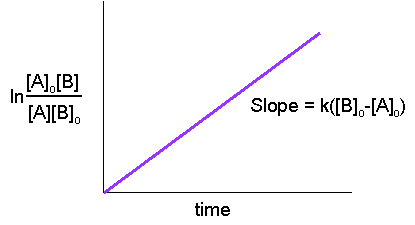
This graph tin can be used in the aforementioned manner as the graph in the department above or written in the other mode:
\[\ln\dfrac{[A]}{[B]} = grand([A]_o - [B]_o)t+\ln\dfrac{[A]_o}{[B]_o}\nonumber \]
in form \( y = ax + b\) with a gradient of \(a= chiliad([B]_0-[A]_0)\) and a y-intercept of \( b = \ln \dfrac{[A]_0}{[B]_0}\)
Situation 2b: \([A]_0 =[B]_0\)
Because \(A + B \rightarrow P\)
Since \(A\) and \(B\) react with a 1 to ane stoichiometry, \([A]= [A]_0 -x\) and \([B] = [B]_0 -x\)
at any time \(t\), \([A] = [B]\) and the charge per unit law will be,
\[\text{rate} = grand[A][B] = k[A][A] = k[A]^2.\nonumber \]
Thus, it is assumed equally the outset case!!!
Example \(\PageIndex{1}\)
The following chemical equation reaction represents the thermal decomposition of gas \(E\) into \(K\) and \(G\) at 200° C
\[\ce{ 5E(g) -> 4K(g) + Chiliad(g)} \nonumber \]
This reaction follows a second order rate law with regards to \(\ce{East}\). For this reaction suppose that the rate constant at 200° C is equivalent to \(4.0 \times 10^{-2} One thousand^{-i}s^{-one}\) and the initial concentration is \(0.050\; M\). Westwardhat is the initial rate of decomposition of \(\ce{E}\).
Solution
Offset by defining the reaction rate in terms of the loss of reactants
\[ \text{Rate (initial)} = - \dfrac{one}{5} \dfrac{d[Eastward]}{dt}\nonumber \]
and and then use the rate constabulary to define the rate of loss of \(\ce{E}\)
\[ \dfrac{d[E]}{dt} = -k [A]_i^2 \nonumber \]
We already know \(k\) and \([A]_i\) simply we need to figure out \(x\). To exercise this await at the units of \(g\) and ane sees it is M-1southward-1 which means the overall reaction is a second lodge reaction with \(x=two\).
\[\begin{align*} \text{Initial charge per unit} &= (4.0 \times 10^{-two} M^{-1}southward^{-1})(0.050\,M)^2 \\[4pt] &= one \times 10^{-4} \, Ms^{-ane}\finish{marshal*} \]
One-half-Life
Another characteristic used to make up one's mind the order of a reaction from experimental data is the one-half-life (\(t_{1/2}\)). Past definition, the half life of any reaction is the amount of fourth dimension it takes to consume one-half of the starting material. For a second-order reaction, the half-life is inversely related to the initial concentration of the reactant (A). For a 2nd-lodge reaction each half-life is twice every bit long as the life span of the one earlier.
Consider the reaction \(2A \rightarrow P\):
We tin can find an expression for the half-life of a second order reaction by using the previously derived integrated rate equation.
\[\dfrac{1}{[A]_t} - \dfrac{1}{[A]_o} = kt \nonumber\]
Since,
\[[A]_{t_{1/2}} = \dfrac{1}{2}[A]_o \nonumber\]
when \(t = t_{1/two} \).
Our integrated rate equation becomes:
\[\dfrac{1}{\dfrac{1}{two}[A]_o} - \dfrac{1}{[A]_o} = kt_{1/2} \nonumber\]
Afterwards a series of algebraic steps,
\[\brainstorm{marshal*} \dfrac{2}{[A]_o} - \dfrac{1}{[A]_o} &= kt_{1/2} \\[4pt] \dfrac{i}{[A]_o} &= kt_{one/two} \terminate{align*}\]
We obtain the equation for the one-half-life of a second order reaction:
\[t_{1/ii} = \dfrac{1}{k[A]_o} \label{second halflife}\]
This changed human relationship suggests that as the initial concentration of reactant is increased, there is a higher probability of the ii reactant molecules interacting to grade product. Consequently, the reactant will be consumed in a shorter amount of time, i.e. the reaction will have a shorter one-half-life. This equation also implies that since the one-half-life is longer when the concentrations are low, species decaying according to 2d-guild kinetics may exist for a longer corporeality of time if their initial concentrations are small-scale.
Note that for the second scenario in which \(A + B \rightarrow P\), the half-life of the reaction cannot exist adamant. As stated earlier, \([A]_o\) cannot be equal to \([B]_o\). Hence, the time it takes to eat one-half of A is not the same as the fourth dimension it takes to consume one-one-half of B. Because of this, we cannot define a full general equation for the half-life of this type of 2nd-gild reaction.
Example \(\PageIndex{2}\): Half-Life of a Second-Order Reaciton
If the only reactant is the initial concentration of \(A\), and information technology is equivalent to \([A]_0=4.l \times 10^{-5}\,One thousand\) and the reaction is a second order with a rate constant \(thou=0.89 M^{-i}s^{-1}\). What is the half-life of this reaction?
Solution
This is a direct application of equation \ref{2d halflife}.
\[\begin{align*} \dfrac{1}{one thousand[A]_0} &= \dfrac{1}{(four.l \times 10^{-v} One thousand)(0.89 M^{-1}{s^{-i})}} \\[4pt] &= 2.50 \times ten^4 \,south \terminate{align*}\]
Summary
| \(2A \rightarrow P\) | \(A + B \rightarrow P\) | |
|---|---|---|
| Differential Form | \(-\dfrac{d[A]}{dt} = yard[A]^2\) | \(-\dfrac{d[A]}{dt} = k[A][B]\) |
| Integral Form | \(\dfrac{one}{[A]_t} = kt + \dfrac{1}{[A]_o}\) | \(\dfrac{1}{[B]_o - [A]_o}\ln\dfrac{[B][A]_o}{[A][B]_o} = kt\) |
| Half Life | \(t_{i/2} = \dfrac{i}{k[A]_o}\) | Cannot be hands defined; \(t_{1/2}\) for A and B are different. |
The graph below is the graph that tests if a reaction is second guild. The reaction is 2nd order if the graph has a straight line, every bit is in the example below.

Practice Problems
1. Given the following information, determine the club of the reaction and the value of k, the reaction constant.
| Concentration (M) | Fourth dimension (s) |
|---|---|
| 1.0 | 10 |
| 0.50 | 20 |
| 0.33 | xxx |
*Hint: Begin by graphing
2. Using the post-obit information, make up one's mind the one-half life of this reaction, assuming there is a unmarried reactant.
| Concentration (M) | Time (s) |
|---|---|
| 2.0 | 0 |
| 1.3 | ten |
| 0.9633 | 20 |
three. Given the information from the previous trouble, what is the concentration after v minutes?
Solutions
one
- Make graphs of concentration vs. time (zeroth guild), natural log of concentration vs. time (first order), and one over concentration vs. fourth dimension (second social club).
- Determine which graph results in a straight line. This graph reflects the order of the reaction. For this problem, the straight line should exist in the 3rd graph, meaning the reaction is second social club.
- The numbers should accept are:
| 1/Concentration(Thousand-i) | Fourth dimension (s) |
|---|---|
| i | ten |
| 2 | xx |
| three | thirty |
The slope can be found past taking the "ascension" over the "run". This means taking 2 points, (ten,1) and (xx,2). The "ascent" is the vertical distance between the points (2-one=1) and the "run" is the horizontal distance (20-10=10). Therefore the slope is 1/x=0.ane. The value of k, therefore, is 0.one Yard-iis-1.
2
- Determine the order of the reaction and the reaction abiding, chiliad, for the reaction using the tactics described in the previous problem. The order of the reaction is second, and the value of k is 0.0269 M-iisouth-1.
- Since the reaction social club is second, the formula for t1/two = chiliad-i[A]o -1. This means that the one-half life of the reaction is 0.0259 seconds.
three
- Convert the time (v minutes) to seconds. This means the time is 300 seconds.
- Use the integrated rate law to notice the final concentration. The concluding concentration is .1167 M.
References
- Atkins, P. W., & De Paula, J. (2006). Physical Chemistry for the Life Sciences. New York, NY: W. H. Freeman and Company.
- Petrucci, R. H., Harwood, Westward. S., & Herring, F. G. (2002). General Chemistry: Principles and Modern Applications. Upper Saddle River, NJ: Prentice-Hall, Inc.
Contributors and Attributions
- Lannah Lua, Ciara Murphy, Victoria Blanchard
thomasyoultaithe94.blogspot.com
Source: https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Supplemental_Modules_%28Physical_and_Theoretical_Chemistry%29/Kinetics/02:_Reaction_Rates/2.08:_Second-Order_Reactions
0 Response to "what happens to the rate when [a] is doubled if x=0"
Post a Comment